Insertion Sort - 插入排序

核心：通过构建有序序列，对于未排序序列，在已排序序列中从后向前扫描(对于单向链表则只能从前往后遍历)，找到相应位置并插入。实现上通常使用in-place排序(需用到O(1)的额外空间)

从第一个元素开始，该元素可认为已排序
取下一个元素，对已排序数组从后往前扫描
若从排序数组中取出的元素大于新元素，则移至下一位置
重复步骤3，直至找到已排序元素小于或等于新元素的位置
插入新元素至该位置
重复2~5

性质：

交换操作和数组中倒置的数量相同
比较次数>=倒置数量，<=倒置的数量加上数组的大小减一
每次交换都改变了两个顺序颠倒的元素的位置，即减少了一对倒置，倒置数量为0时即完成排序。
每次交换对应着一次比较，且1到N-1之间的每个i都可能需要一次额外的记录(a[i]未到达数组左端时)
最坏情况下需要~~N^2/2次比较和~~N^2/2次交换，最好情况下需要N-1次比较和0次交换。
平均情况下需要~~N^2/4次比较和~~N^2/4次交换

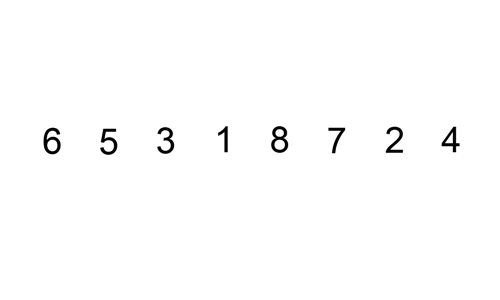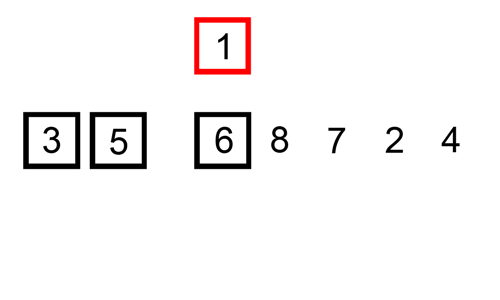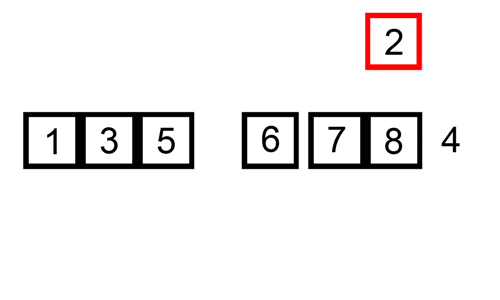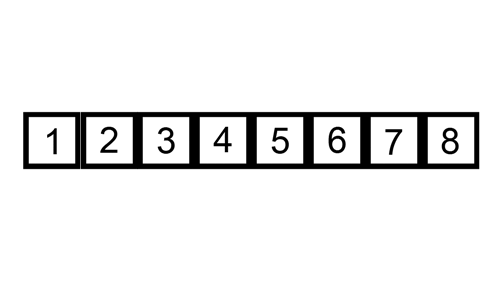
Insertion Sort

Implementation

Python

#!/usr/bin/env python


def insertionSort(alist):
    for i, item_i in enumerate(alist):
        print alist
        index = i
        while index > 0 and alist[index - 1] > item_i:
            alist[index] = alist[index - 1]
            index -= 1

        alist[index] = item_i

    return alist

unsorted_list = [6, 5, 3, 1, 8, 7, 2, 4]
print(insertionSort(unsorted_list))
copy

Java

public class Sort {
    public static void main(String[] args) {
        int unsortedArray[] = new int[]{6, 5, 3, 1, 8, 7, 2, 4};
        insertionSort(unsortedArray);
        System.out.println("After sort: ");
        for (int item : unsortedArray) {
            System.out.print(item + " ");
        }
    }

    public static void insertionSort(int[] array) {
        int len = array.length;
        for (int i = 0; i < len; i++) {
            int index = i, array_i = array[i];
            while (index > 0 && array[index - 1] > array_i) {
                array[index] = array[index - 1];
                index -= 1;
            }
            array[index] = array_i;

            /* print sort process */
            for (int item : array) {
                System.out.print(item + " ");
            }
            System.out.println();
        }
    }
}
copy

实现(C++)：

template<typename T>
void insertion_sort(T arr[], int len) {
    int i, j;
    T temp;
    for (int i = 1; i < len; i++) {
        temp = arr[i];
        for (int j = i - 1; j >= 0 && arr[j] > temp; j--) {
            a[j + 1] = a[j];
        }
        arr[j + 1] = temp;
    }
}
copy

希尔排序

核心：基于插入排序，使数组中任意间隔为h的元素都是有序的，即将全部元素分为h个区域使用插入排序。其实现可类似于插入排序但使用不同增量。更高效的原因是它权衡了子数组的规模和有序性。

实现(C++):

template<typename T>
void shell_sort(T arr[], int len) {
    int gap, i, j;
    T temp;
    for (gap = len >> 1; gap > 0; gap >>= 1)
        for (i = gap; i < len; i++) {
            temp = arr[i];
            for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)
                arr[j + gap] = arr[j];
            arr[j + gap] = temp;
        }
}
copy

Insertion Sort - 插入排序

Implementation

Python

Java

希尔排序

Reference