Problem B. Professor Q's Software

Source

• hihoCoder

Problem

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

Professor Q develops a new software. The software consists of N modules which are numbered from 1 to N. The i-th module will be started up by signal Si. If signal Si is generated multiple times, the i-th module will also be started multiple times. Two different modules may be started up by the same signal. During its lifecircle, the i-th module will generate Ki signals: E1, E2, ..., EKi. These signals may start up other modules and so on. Fortunately the software is so carefully designed that there is no loop in the starting chain of modules, which means eventually all the modules will be stoped. Professor Q generates some initial signals and want to know how many times each module is started.

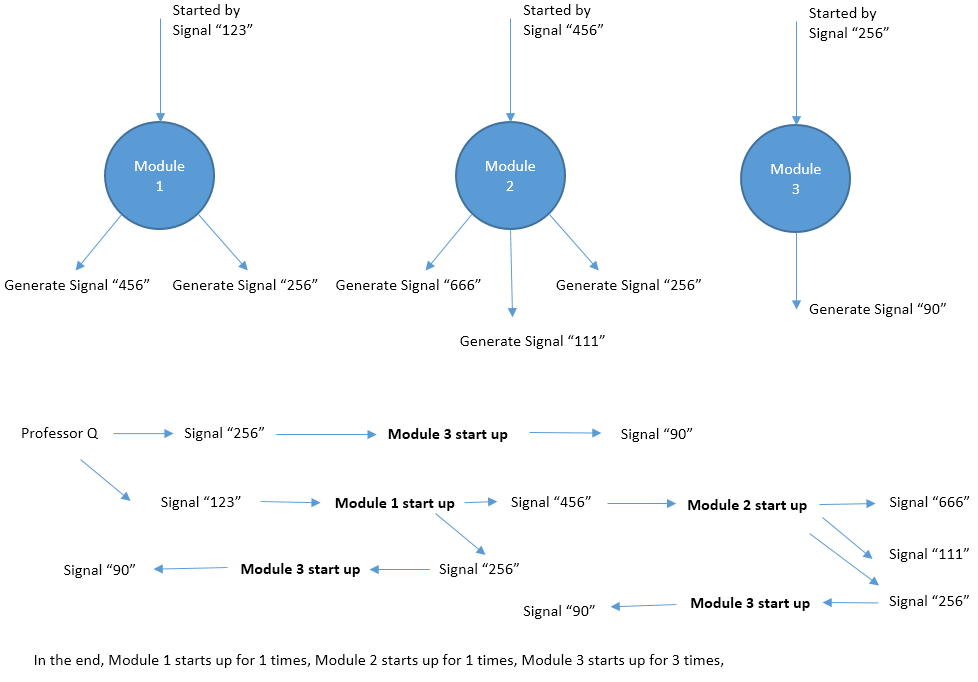
输入

The first line contains an integer T, the number of test cases. T test cases follows.

For each test case, the first line contains contains two numbers N and M, indicating the number of modules and number of signals that Professor Q generates initially.

The second line contains M integers, indicating the signals that Professor Q generates initially.

Line 3~N + 2, each line describes an module, following the format S, K, E1, E2, ... , EK. S represents the signal that start up this module. K represents the total amount of signals that are generated during the lifecircle of this module. And E1 ... EK are these signals.

For 20% data, all N, M <= 10 For 40% data, all N, M <= 103 For 100% data, all 1 <= T <= 5, N, M <= 105, 0 <= K <= 3, 0 <= S, E <= 105.

Hint: HUGE input in this problem. Fast IO such as scanf and BufferedReader are recommended.

输出

For each test case, output a line with N numbers Ans1, Ans2, ... , AnsN. Ansi is the number of times that the i-th module is started. In case the answers may be too large, output the answers modulo 142857 (the remainder of division by 142857).

样例输入

3
3 2
123 256
123 2 456 256
456 3 666 111 256
256 1 90
3 1
100
100 2 200 200
200 1 300
200 0
5 1
1
1 2 2 3
2 2 3 4
3 2 4 5
4 2 5 6
5 2 6 7
copy

样例输出

1 1 3
1 2 2
1 1 2 3 5
copy